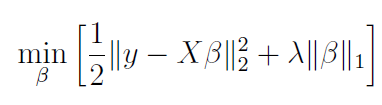Implementation of methods from "Gradient methods for minimizing composite functions" by Yu. Nesterov for minimization problem:

where y is a vector of observations (empirical data) of endogenous variables, X is a matrix of observations of exogenous variables, beta is a vector of model's parameters and lambda is a penalty parameter.

link to paper: https://link.springer.com/article/10.1007/s10107-012-0629-5

Please note that some transformations were needed to obtain a method from the paper above (like three pages of them). They are included in the pdf file.

Conclusions:

• Accelerated Method were always the fastest to converge, both in terms of number of steps and computation time.
• Basic Method and Dual Gradient Method always converged in the same pace when it comes to the number of steps.
• Basic Method execution was slightly faster, causing a very small lead over Dual Gradient Method in convergence time.
• In all tests, all three methods converged to the same final results.
• The way methods estimated the Lipschitz constant differed throughout the problems. Accelerated Method tended to use higher estimations than the other two methods.
• Values of gamma_u did not have a significant impact on the models' performance.
• Values of gamma_u had a huge impact on the models' execution time. Raising gamma_u was causing the execution time to drop significantly.